
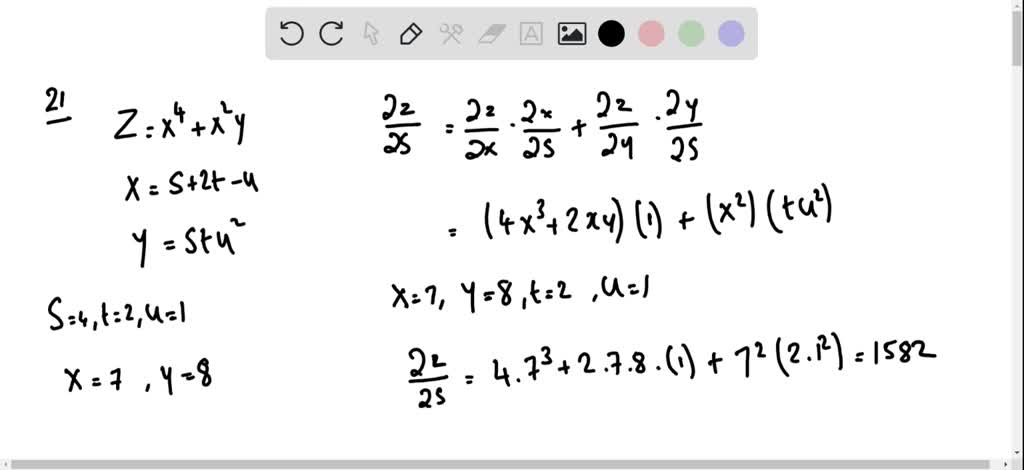
14 5 The Chain Rule For Multivariable Functions Mathematics Libretexts
√ダウンロード u=(x^2 y^2 z^2)^1/2 partial derivative 2772 Problem 90 The heat equation An important partial differential equation that describes the distribution of heat in a region at time t can be represented by the onedimensional heat equation ∂f ∂t = ∂2f ∂x2 Show that u(x, t) = sin(αx) ⋅ e − βt satisfies the heatPartial derivative and gradient (articles) Introduction to partial derivatives This is the currently selected item Second partial derivatives The gradient Directional derivatives (introduction) Directional derivatives (going deeper) Next lesson Differentiating parametric curves Sort by
U=(x^2 y^2 z^2)^-1/2 partial derivative
U=(x^2 y^2 z^2)^-1/2 partial derivative- In this case we call h′(b) h ′ ( b) the partial derivative of f (x,y) f ( x, y) with respect to y y at (a,b) ( a, b) and we denote it as follows, f y(a,b) = 6a2b2 f y ( a, b) = 6 a 2 b 2 Note that these two partial derivatives are sometimes called the first order partial derivatives Just as with functions of one variable we can haveℓ n (t) = {x = 0 y =2 t 1 z =t 1 As mentioned when studying the total differential, it is not uncommon to know partial derivative information about an unknown function, and tangent planes are used to give accurate approximations of the function

If U X 2tan 1 Y X Y 2tan 1 X Y Then Find 2u X Y
Partial Derivatives and their Applications 265 Solution Given ( )2/2 2 2 22 m Vr r x y z== =mm (1) Here V xx denotes 2nd order partial derivative of V(x, y, z) with respect to x keeping y and z constant Thus ==∂∂ − ∂∂ (, z=,) ( ) ( ) 222 2 2 2 2221 22 PARTIAL DIFFERENTIATION 1 b) wx = −y2/x2, wy = 2y/x;EXAMPLE 1415 Suppose the temperature at (x,y,z) is T(x,y,z) = e−(x2y2z2) This function has a maximum value of 1 at the origin, and tends to 0 in all directions If k is positive and at most 1, the set of points for which T(x,y,z) = k is those points satisfying x 2y2 z = −lnk, a sphere centered at the origin The level surfaces are the
Partial Differential Equations Igor Yanovsky, 05 3 Contents 1 Trigonometric Identities 6 2 Simple Eigenvalue Problem 8 3 Separation of Variables y = t, z = h(s) u(x,y)=h(x−uy) (52) The characteristic projection in the xtplane1 passing through the point (s,0) is the line x = h(s)ts (delw)/(delx) = x/sqrt(x^2 y^2 z^2) (delw)/(dely) = y/sqrt(x^2 y^2 z^2) (delw)/(delz) = z/sqrt(x^2 y^2 z^2) Since you're dealing with a multivariable function, you must treat x, y, and z as independent variables and calculate the partial derivative of w, your dependent variable, with respect to x, y, and z When you differentiate with respect to x, you treat y and z Example 1 Find each of the directional derivatives D→u f (2,0) D u → f ( 2, 0) where f (x,y) = xexy y f ( x, y) = x e x y y and →u u → is the unit vector in the direction of θ = 2π 3 θ = 2 π 3 D→u f (x,y,z) D u → f ( x, y, z) where f (x,y,z) = x2zy3z2 −xyz f ( x, y, z) = x 2 z y 3 z 2 − x y z in the direction of →v
U=(x^2 y^2 z^2)^-1/2 partial derivativeのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 | 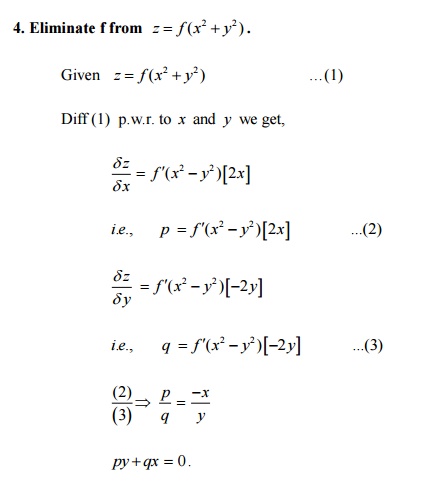 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
「U=(x^2 y^2 z^2)^-1/2 partial derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 | 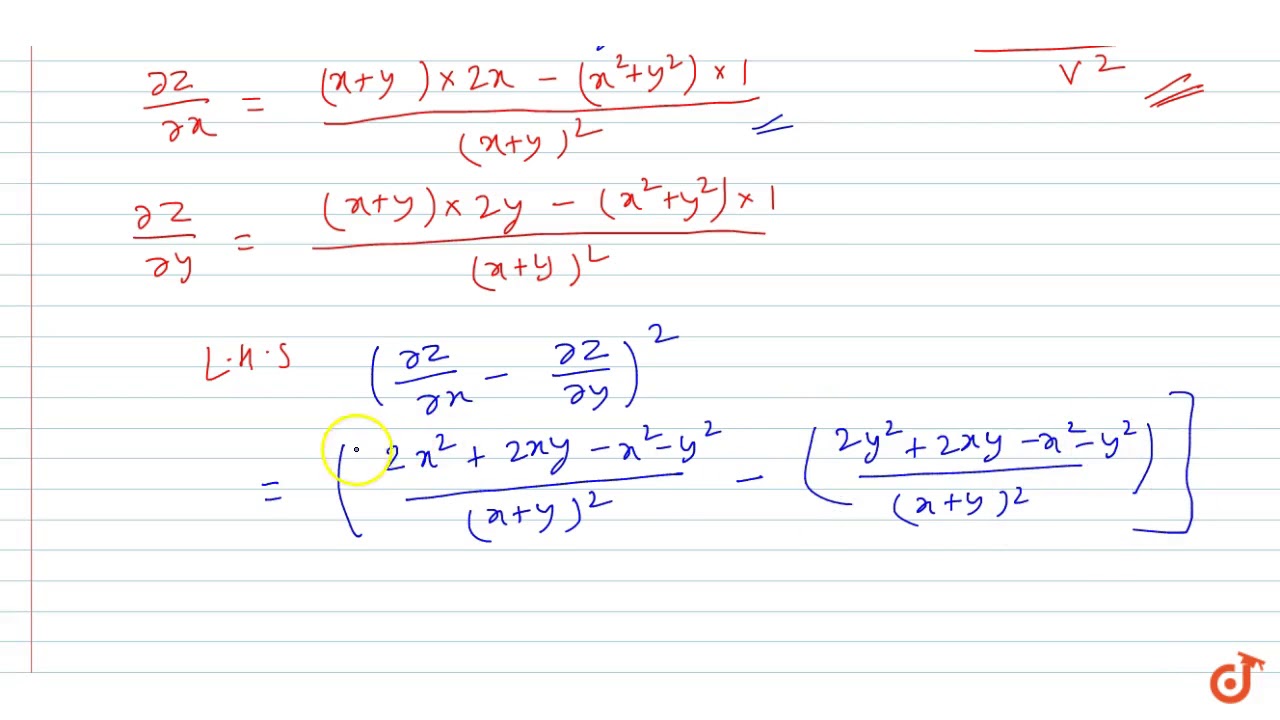 Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
「U=(x^2 y^2 z^2)^-1/2 partial derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 | 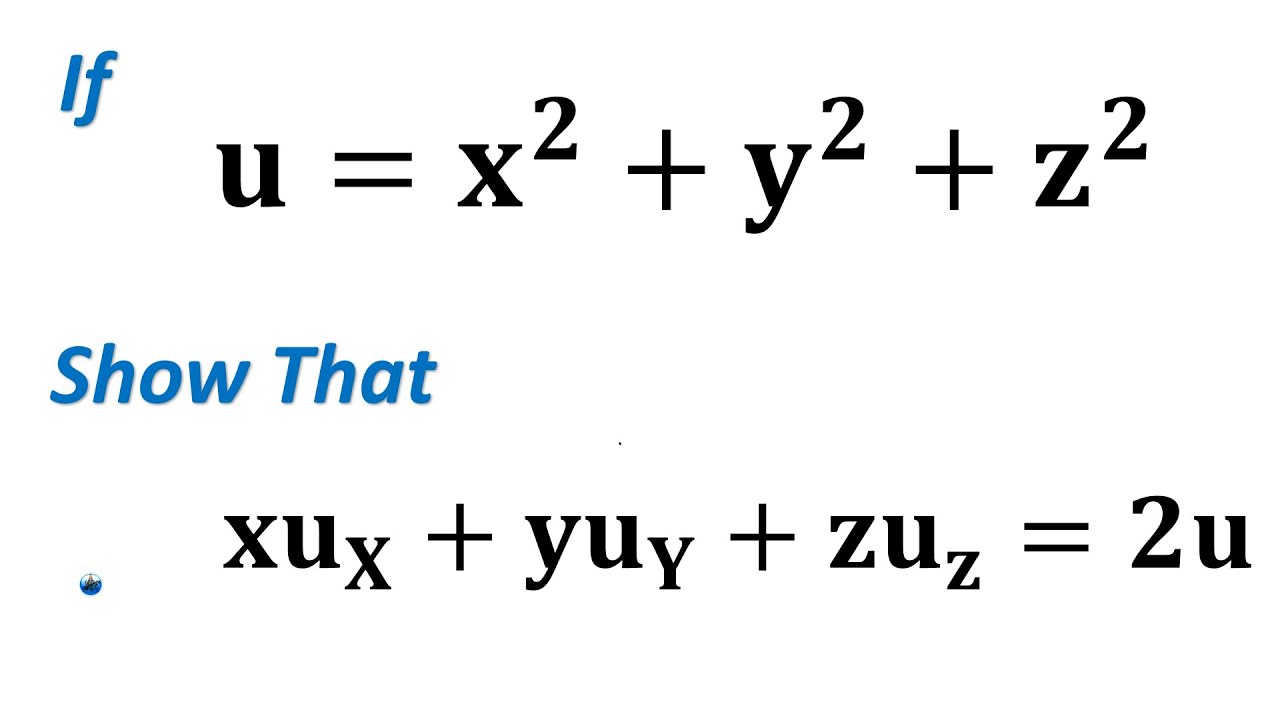 Partial Derivatives Calculus 3 |
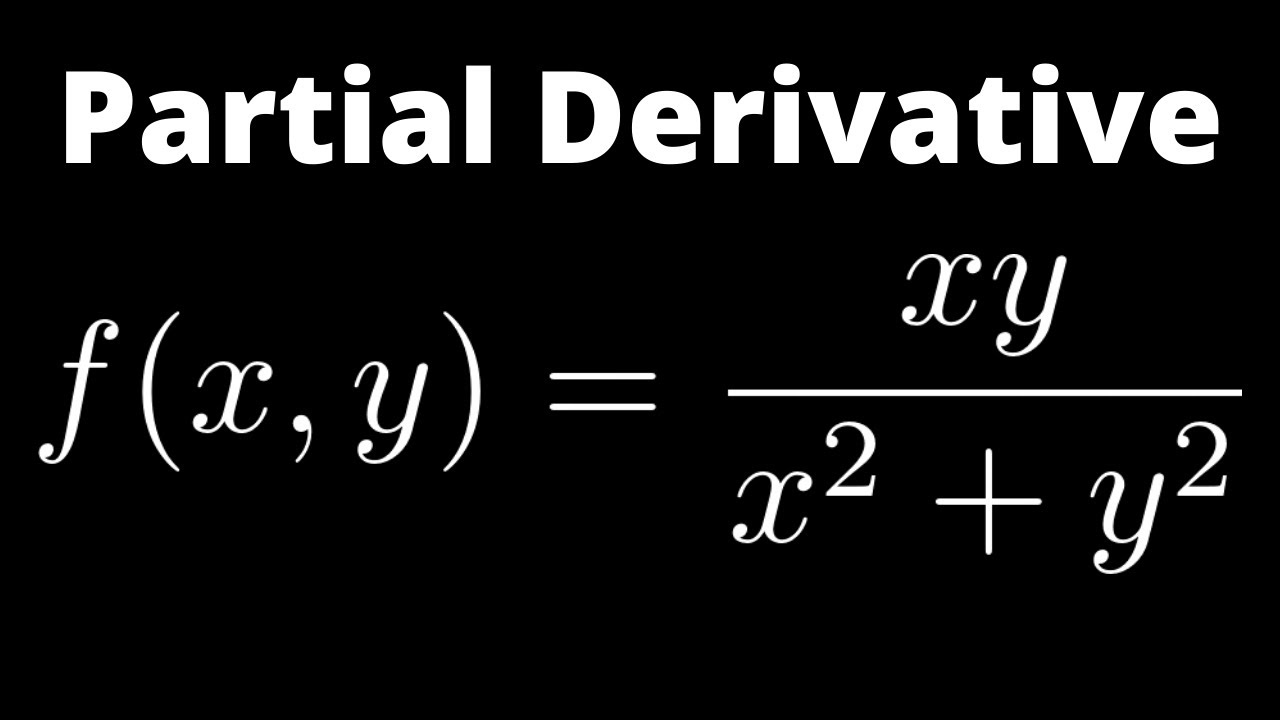 Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
「U=(x^2 y^2 z^2)^-1/2 partial derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |
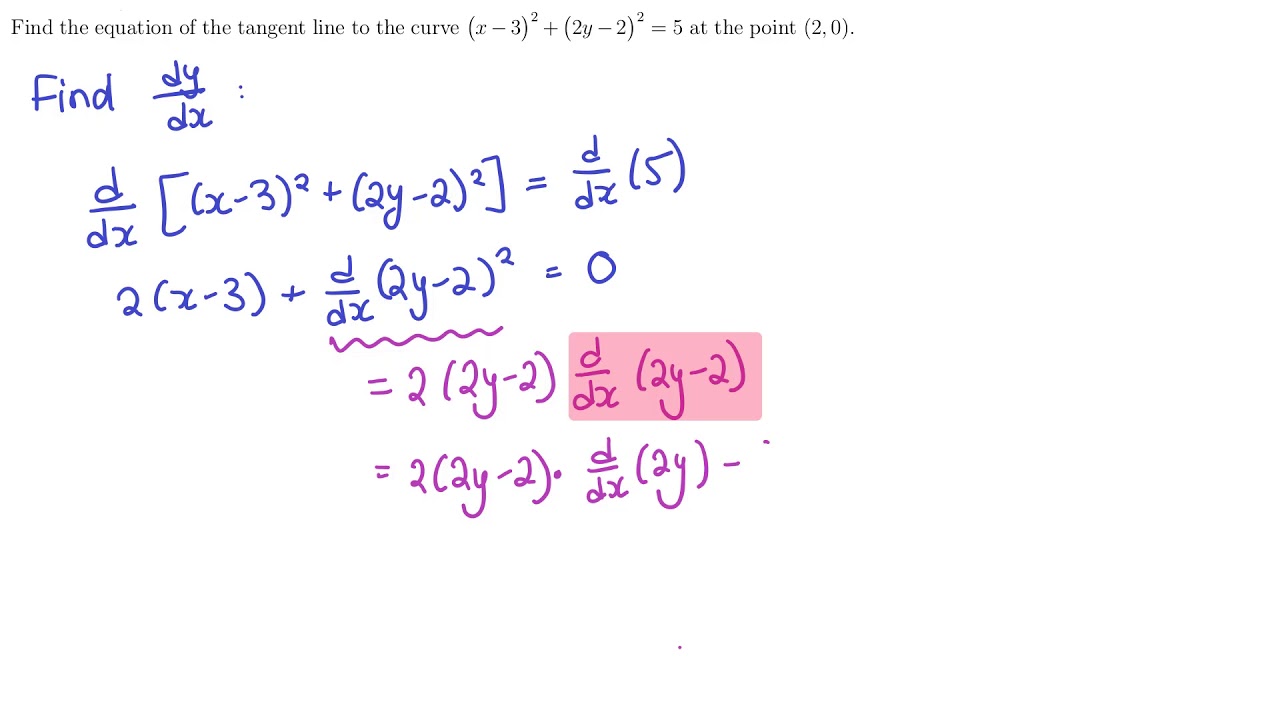 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
「U=(x^2 y^2 z^2)^-1/2 partial derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
「U=(x^2 y^2 z^2)^-1/2 partial derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 | 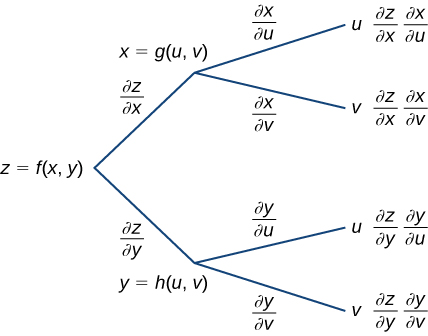 Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
「U=(x^2 y^2 z^2)^-1/2 partial derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
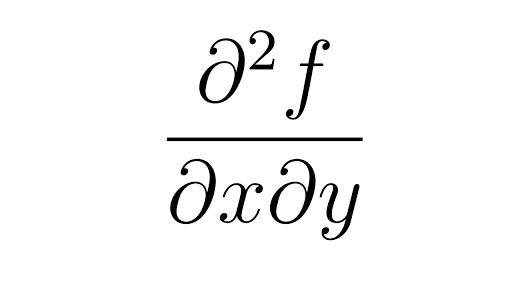 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |
「U=(x^2 y^2 z^2)^-1/2 partial derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 | 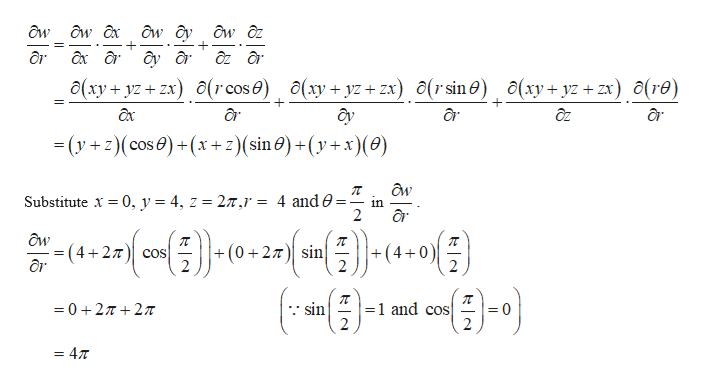 Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
「U=(x^2 y^2 z^2)^-1/2 partial derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |
「U=(x^2 y^2 z^2)^-1/2 partial derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 | 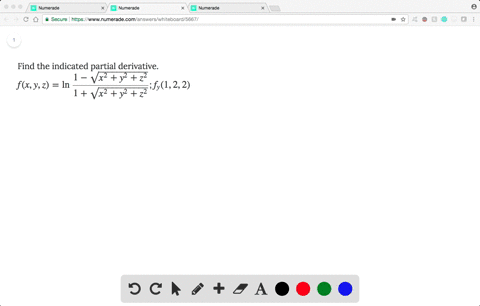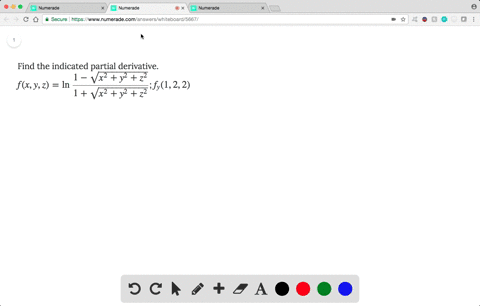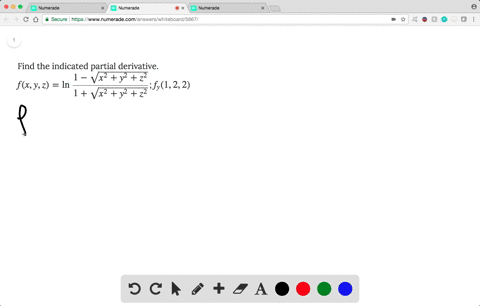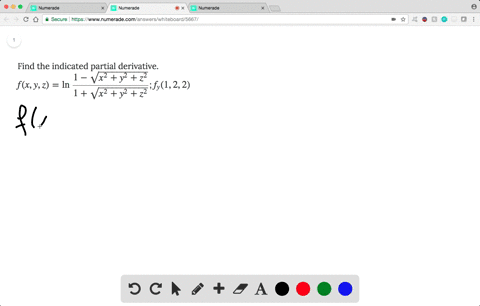 Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
「U=(x^2 y^2 z^2)^-1/2 partial derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 | Partial Derivatives Calculus 3 |
「U=(x^2 y^2 z^2)^-1/2 partial derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
 Partial Derivatives Calculus 3 |  Partial Derivatives Calculus 3 |
Partial Derivative Formulas and Identities There are some identities for partial derivatives as per the definition of the function 1 If u = f (x,y) and both x and y are differentiable of t ie x = g (t) and y = h (t), then the term differentiation becomes total differentiation 2By the Sum Rule, the derivative of x2 y2 z2 x 2 y 2 z 2 with respect to x x is d dx x2 d dx y2 d dx z2 d d x x 2 d d x y 2 d d x z 2 Differentiate using the Power Rule which states that d dx xn d d x x n is nxn−1 n x n 1 where n = 2 n = 2 Since y2 y 2 is constant with respect to x x, the derivative of y2 y





0 件のコメント:
コメントを投稿